---
# Mode Decomposition
---

This tutorial demonstrates the [mode-decomposition](../Mode_Decomposition.md) feature which is used to decompose a given mode profile via the Fourier-transformed fields into a superposition of harmonic basis modes. Examples are provided for two kinds of modes in lossless, dielectric media: (1) localized (i.e., guided) and (2) non-localized (i.e., radiative planewave).

[TOC]

Reflectance of a Waveguide Taper
--------------------------------

This example involves computing the reflectance of the fundamental mode of a linear waveguide taper. The structure and the simulation parameters are shown in the schematic below. We will verify that computing the reflectance, the fraction of the incident power which is reflected, using two different methods produces nearly identical results: (1) mode decomposition and (2) [Poynting flux](../Introduction.md#transmittancereflectance-spectra). Also, we will demonstrate that the scaling of the reflectance with the taper length is quadratic, consistent with analytical results from [Optics Express, Vol. 16, pp. 11376-92 (2008)](http://www.opticsinfobase.org/abstract.cfm?URI=oe-16-15-11376).


![](../images/waveguide-taper.png#center)



The structure, which can be viewed as a [two-port network](https://en.wikipedia.org/wiki/Two-port_network), consists of a single-mode waveguide of width 1 μm (`w1`) at a wavelength of 6.67 μm and coupled to a second waveguide of width 2 μm (`w2`) via a linearly-sloped taper of variable length `Lt`. The material is silicon with $\varepsilon=12$. The taper geometry is defined using a single [`Prism`](../Python_User_Interface.md#prism) object with eight vertices. PML absorbing boundaries surround the entire cell. An eigenmode current source with $E_z$ (or $\mathcal{S}$) polarization is used to launch the fundamental mode. The dispersion relation (or "band diagram") of the single-mode waveguide is shown in [Tutorial/Eigenmode Source](Eigenmode_Source.md). There is an eigenmode-expansion monitor placed at the midpoint of the first waveguide. This is a line monitor which extends beyond the waveguide in order to span the entire mode profile including its evanescent tails. The Fourier-transformed fields along this line monitor are used to compute the basis coefficients of the harmonic modes. These are computed separately via the eigenmode solver [MPB](https://mpb.readthedocs.io/en/latest/). This is described in [Mode Decomposition](../Mode_Decomposition.md) where it is also shown that the squared magnitude of the mode coefficient is equivalent to the power (Poynting flux) in the given eigenmode. The ratio of the complex mode coefficients can be used to compute the [S parameters](https://en.wikipedia.org/wiki/Scattering_parameters). In this example, we are computing $|S_{11}|^2$ which is the reflectance (shown in the line prefixed by "refl:,"). Another line monitor could have been placed in the second waveguide to compute the transmittance or $|S_{21}|^2$ into the various guided modes (since the second waveguide is multi mode). The scattered power into the radiative modes can then be computed as $1-|S_{11}|^2-|S_{21}|^2$. As usual, a normalization run is required involving a straight waveguide to compute the power in the source.

The structure has mirror symmetry in the $y$ direction which can be exploited to reduce the computation size by a factor of two. This requires using `add_flux` rather than `add_mode_monitor` (which is not optimized for symmetry) and specifying the keyword argument `eig_parity=mp.ODD_Z+mp.EVEN_Y` in the call to `get_eigenmode_coefficients`. Alternatively, the waveguide could have been oriented along an arbitrary oblique direction which would require specifying `direction=mp.NO_DIRECTION` and `kpoint_func` as the waveguide axis. For an example, see [Tutorials/Eigenmode Source/Index-Guided Modes in a Ridge Waveguide](Eigenmode_Source.md#index-guided-modes-in-a-ridge-waveguide).

The simulation script is in [examples/mode-decomposition.py](https://github.com/NanoComp/meep/blob/master/python/examples/mode-decomposition.py). The notebook is [examples/mode-decomposition.ipynb](https://nbviewer.jupyter.org/github/NanoComp/meep/blob/master/python/examples/mode-decomposition.ipynb).

```py
import meep as mp
import matplotlib.pyplot as plt

resolution = 25   # pixels/μm

w1 = 1.0          # width of waveguide 1
w2 = 2.0          # width of waveguide 2
Lw = 10.0         # length of waveguides 1 and 2

# lengths of waveguide taper
Lts = [2**m for m in range(4)]

dair = 3.0        # length of air region
dpml_x = 6.0      # length of PML in x direction
dpml_y = 2.0      # length of PML in y direction

sy = dpml_y+dair+w2+dair+dpml_y

Si = mp.Medium(epsilon=12.0)

boundary_layers = [mp.PML(dpml_x,direction=mp.X),
                   mp.PML(dpml_y,direction=mp.Y)]

lcen = 6.67       # mode wavelength
fcen = 1/lcen     # mode frequency

symmetries = [mp.Mirror(mp.Y)]

R_coeffs = []
R_flux = []

for Lt in Lts:
    sx = dpml_x+Lw+Lt+Lw+dpml_x
    cell_size = mp.Vector3(sx,sy,0)

    src_pt = mp.Vector3(-0.5*sx+dpml_x+0.2*Lw)
    sources = [mp.EigenModeSource(src=mp.GaussianSource(fcen,fwidth=0.2*fcen),
                                  center=src_pt,
                                  size=mp.Vector3(y=sy-2*dpml_y),
                                  eig_match_freq=True,
                                  eig_parity=mp.ODD_Z+mp.EVEN_Y)]

    # straight waveguide
    vertices = [mp.Vector3(-0.5*sx-1,0.5*w1),
                mp.Vector3(0.5*sx+1,0.5*w1),
                mp.Vector3(0.5*sx+1,-0.5*w1),
                mp.Vector3(-0.5*sx-1,-0.5*w1)]

    sim = mp.Simulation(resolution=resolution,
                        cell_size=cell_size,
                        boundary_layers=boundary_layers,
                        geometry=[mp.Prism(vertices,height=mp.inf,material=Si)],
                        sources=sources,
                        symmetries=symmetries)

    mon_pt = mp.Vector3(-0.5*sx+dpml_x+0.7*Lw)
    flux = sim.add_flux(fcen,0,1,mp.FluxRegion(center=mon_pt,size=mp.Vector3(y=sy-2*dpml_y)))

    sim.run(until_after_sources=mp.stop_when_fields_decayed(50,mp.Ez,mon_pt,1e-9))

    res = sim.get_eigenmode_coefficients(flux,[1],eig_parity=mp.ODD_Z+mp.EVEN_Y)
    incident_coeffs = res.alpha
    incident_flux = mp.get_fluxes(flux)
    incident_flux_data = sim.get_flux_data(flux)

    sim.reset_meep()

    # linear taper
    vertices = [mp.Vector3(-0.5*sx-1,0.5*w1),
                mp.Vector3(-0.5*Lt,0.5*w1),
                mp.Vector3(0.5*Lt,0.5*w2),
                mp.Vector3(0.5*sx+1,0.5*w2),
                mp.Vector3(0.5*sx+1,-0.5*w2),
                mp.Vector3(0.5*Lt,-0.5*w2),
                mp.Vector3(-0.5*Lt,-0.5*w1),
                mp.Vector3(-0.5*sx-1,-0.5*w1)]

    sim = mp.Simulation(resolution=resolution,
                        cell_size=cell_size,
                        boundary_layers=boundary_layers,
                        geometry=[mp.Prism(vertices,height=mp.inf,material=Si)],
                        sources=sources,
                        symmetries=symmetries)

    flux = sim.add_flux(fcen,0,1,mp.FluxRegion(center=mon_pt,size=mp.Vector3(y=sy-2*dpml_y)))
    sim.load_minus_flux_data(flux,incident_flux_data)

    sim.run(until_after_sources=mp.stop_when_fields_decayed(50,mp.Ez,mon_pt,1e-9))

    res = sim.get_eigenmode_coefficients(flux,[1],eig_parity=mp.ODD_Z+mp.EVEN_Y)
    taper_coeffs = res.alpha
    taper_flux = mp.get_fluxes(flux)

    R_coeffs.append(abs(taper_coeffs[0,0,1])**2/abs(incident_coeffs[0,0,0])**2)
    R_flux.append(-taper_flux[0]/incident_flux[0])
    print("refl:, {}, {:.8f}, {:.8f}".format(Lt,R_coeffs[-1],R_flux[-1]))
```

Note that the reflectance is computed for five different geometrically-scaled taper lengths: 1, 2, 4, 8, and 16 μm. A quadratic scaling of the reflectance with the taper length appears as a straight line on a log-log plot. The results are plotted using the commands below with the plot shown in the accompanying figure.

```py
if mp.am_master():
    plt.figure()
    plt.loglog(Lts,R_coeffs,'bo-',label='mode decomposition')
    plt.loglog(Lts,R_flux,'ro-',label='Poynting flux')
    plt.loglog(Lts,[0.005/Lt**2 for Lt in Lts],'k-',label=r'quadratic reference (1/Lt$^2$)')
    plt.legend(loc='upper right')
    plt.xlabel('taper length Lt (μm)')
    plt.ylabel('reflectance')
    plt.show()
```

![](../images/refl_coeff_vs_taper_length.png#center)



The reflectance values computed using the two methods are nearly identical. For reference, a line with quadratic scaling is shown in black. The reflectance of the linear waveguide taper decreases quadratically with the taper length which is consistent with the analytic theory.

In the reflected-flux calculation, we apply our usual trick of first performing a reference simulation with just the incident field and then subtracting that from our taper simulation with `load_minus_flux_data`, so that what is left over is the reflected fields (from which we obtain the reflected flux).  In *principle*, this trick would not be required for the mode-decomposition method, because the reflected mode is orthogonal to the forward mode and so the decomposition will separate the forward and reflected coefficients automatically.   However, this is only true in the limit of infinite resolution — for a *finite* resolution, the reflected mode used for the mode coefficient calculation (calculated via MPB) is not exactly orthogonal to the forward mode propagating in Meep (whose discretization scheme is different from that of MPB).   In consequence, if you did not subtract the fields of the reference simulation, the mode-coefficient could only calculate the reflected power down to a "noise floor" set by the discretization error.  With the subtraction, in contrast, you can compute much smaller reflections (limited by the floating-point precision).

Diffraction Spectrum of a Binary Grating
----------------------------------------

The mode-decomposition feature can also be applied to planewaves in homogeneous media with scalar permittivity/permeability (i.e., no anisotropy). This will be demonstrated in this example to compute the diffraction spectrum of a binary phase [grating](https://en.wikipedia.org/wiki/Diffraction_grating). To compute the diffraction spectrum for a finite-length structure, see [Tutorials/Near to Far Field Spectra/Diffraction Spectrum of a Finite Binary Grating](Near_to_Far_Field_Spectra.md#diffraction-spectrum-of-a-finite-binary-grating). The unit cell geometry of the grating is shown in the schematic below. The grating is periodic in the $y$ direction with periodicity `gp` and has a rectangular profile of height `gh` and duty cycle `gdc`. The grating parameters are `gh`=0.5 μm, `gdc`=0.5, and `gp`=10 μm. There is a semi-infinite substrate of thickness `dsub` adjacent to the grating. The substrate and grating are glass with a refractive index of 1.5. The surrounding is air/vacuum. Perfectly matched layers (PML) of thickness `dpml` are used in the $\pm x$ boundaries.

### Transmissive Diffraction Spectrum for Planewave at Normal Incidence

A pulsed planewave with $E_z$ (or $\mathcal{S}$) polarization spanning wavelengths of 0.4 to 0.6 μm is normally incident on the grating from the glass substrate. The eigenmode monitor is placed in the air region. We will use mode decomposition to compute the transmittance — the ratio of the power in the $+x$ direction of the diffracted mode relative to that of the incident planewave — for the first ten diffraction orders. Two simulations are required: (1) an *empty* cell of homogeneous glass to obtain the incident power of the source, and (2) the grating structure to obtain the diffraction orders. At the end of the simulation, the wavelength, angle, and transmittance for each diffraction order are computed.

The simulation script is in [examples/binary_grating.py](https://github.com/NanoComp/meep/blob/master/python/examples/binary_grating.py). The notebook is [examples/binary_grating.ipynb](https://nbviewer.jupyter.org/github/NanoComp/meep/blob/master/python/examples/binary_grating.ipynb).


![](../images/grating.png#center)



```py
import meep as mp
import math
import numpy as np
import matplotlib.pyplot as plt

resolution = 60        # pixels/μm

dpml = 1.0             # PML thickness
dsub = 3.0             # substrate thickness
dpad = 3.0             # padding between grating and PML
gp = 10.0              # grating period
gh = 0.5               # grating height
gdc = 0.5              # grating duty cycle

sx = dpml+dsub+gh+dpad+dpml
sy = gp

cell_size = mp.Vector3(sx,sy,0)
pml_layers = [mp.PML(thickness=dpml,direction=mp.X)]

wvl_min = 0.4           # min wavelength
wvl_max = 0.6           # max wavelength
fmin = 1/wvl_max        # min frequency
fmax = 1/wvl_min        # max frequency
fcen = 0.5*(fmin+fmax)  # center frequency
df = fmax-fmin          # frequency width

src_pt = mp.Vector3(-0.5*sx+dpml+0.5*dsub,0,0)
sources = [mp.Source(mp.GaussianSource(fcen, fwidth=df),
                     component=mp.Ez,
                     center=src_pt,
                     size=mp.Vector3(0,sy,0))]

k_point = mp.Vector3(0,0,0)

glass = mp.Medium(index=1.5)

symmetries=[mp.Mirror(mp.Y)]

sim = mp.Simulation(resolution=resolution,
                    cell_size=cell_size,
                    boundary_layers=pml_layers,
                    k_point=k_point,
                    default_material=glass,
                    sources=sources,
                    symmetries=symmetries)

nfreq = 21
mon_pt = mp.Vector3(0.5*sx-dpml-0.5*dpad,0,0)
flux_mon = sim.add_flux(fcen,
                        df,
                        nfreq,
                        mp.FluxRegion(center=mon_pt, size=mp.Vector3(0,sy,0)))

sim.run(until_after_sources=mp.stop_when_fields_decayed(50, mp.Ez, mon_pt, 1e-9))

input_flux = mp.get_fluxes(flux_mon)

sim.reset_meep()

geometry = [mp.Block(material=glass,
                     size=mp.Vector3(dpml+dsub,mp.inf,mp.inf),
                     center=mp.Vector3(-0.5*sx+0.5*(dpml+dsub),0,0)),
            mp.Block(material=glass,
                     size=mp.Vector3(gh,gdc*gp,mp.inf),
                     center=mp.Vector3(-0.5*sx+dpml+dsub+0.5*gh,0,0))]

sim = mp.Simulation(resolution=resolution,
                    cell_size=cell_size,
                    boundary_layers=pml_layers,
                    geometry=geometry,
                    k_point=k_point,
                    sources=sources,
                    symmetries=symmetries)

mode_mon = sim.add_flux(fcen,
                        df,
                        nfreq,
                        mp.FluxRegion(center=mon_pt, size=mp.Vector3(0,sy,0)))

sim.run(until_after_sources=mp.stop_when_fields_decayed(50, mp.Ez, mon_pt, 1e-9))

freqs = mp.get_eigenmode_freqs(mode_mon)

nmode = 10
res = sim.get_eigenmode_coefficients(mode_mon, range(1,nmode+1), eig_parity=mp.ODD_Z+mp.EVEN_Y)
coeffs = res.alpha
kdom = res.kdom

mode_wvl = []
mode_angle = []
mode_tran = []

for nm in range(nmode):
  for nf in range(nfreq):
    mode_wvl.append(1/freqs[nf])
    mode_angle.append(math.degrees(math.acos(kdom[nm*nfreq+nf].x/freqs[nf])))
    tran = abs(coeffs[nm,nf,0])**2/input_flux[nf]
    mode_tran.append(0.5*tran if nm != 0 else tran)
    print("grating{}:, {:.5f}, {:.2f}, {:.8f}".format(nm,mode_wvl[-1],mode_angle[-1],mode_tran[-1]))
```

Note the use of the keyword parameter argument `eig_parity=mp.ODD_Z+mp.EVEN_Y` in the call to `get_eigenmode_coefficients`. This is important for specifying **non-degenerate** modes in MPB since the `k_point` is (0,0,0). `ODD_Z` is for modes with $E_z$ (or $\mathcal{S}$) polarization. `EVEN_Y` is necessary since each diffraction order which is based on a given $k_x$ consists of *two* modes: one going in the $+y$ direction and the other in the $-y$ direction. `EVEN_Y` forces MPB to compute only the $+k_y + -k_y$ (cosine) mode. As a result, the total transmittance must be halved in this case to obtain the transmittance for the individual $+k_y$ or $-k_y$ mode. For `ODD_Y`, MPB will compute the $+k_y - -k_y$ (sine) mode but this will have zero power because the source is even. If the $y$ parity is left out, MPB will return a random superposition of the cosine and sine modes. Alternatively, in this example an input planewave with $H_z$ instead of $E_z$ polarization can be used which requires `eig_parity=mp.EVEN_Z+mp.ODD_Y` as well as an odd mirror symmetry plane in $y$. Finally, note the use of `add_flux` instead of `add_mode_monitor` when using symmetries.

The diffraction spectrum is then plotted and shown in the figure below.

```py
tran_max = round(max(mode_tran),1)

plt.figure()
plt.pcolormesh(np.reshape(mode_wvl,(nmode,nfreq)),
               np.reshape(mode_angle,(nmode,nfreq)),
               np.reshape(mode_tran,(nmode,nfreq)),
               cmap='Blues',
               shading='nearest',
               vmin=0,
               vmax=tran_max)
plt.axis([min(mode_wvl), max(mode_wvl), min(mode_angle), max(mode_angle)])
plt.xlabel("wavelength (μm)")
plt.ylabel("diffraction angle (degrees)")
plt.xticks([t for t in np.arange(0.4,0.7,0.1)])
plt.yticks([t for t in range(0,35,5)])
plt.title("transmittance of diffraction orders")
cbar = plt.colorbar()
cbar.set_ticks([t for t in np.arange(0,tran_max+0.1,0.1)])
cbar.set_ticklabels(["{:.1f}".format(t) for t in np.arange(0,tran_max+0.1,0.1)])
plt.show()
```

Each diffraction order corresponds to a single angle. In the figure below, this angle is represented by the *lower* boundary of each labeled region. For example, the $m$=0 order has a diffraction angle of 0° at all wavelengths. The representation of the diffraction orders as finite angular regions is an artifact of matplotlib's [pcolormesh](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.pcolormesh.html) routine. Note that only the positive diffraction orders are shown as these are equivalent to the negative orders due to the symmetry of the source and the structure.

The diffraction orders/modes are a finite set of propagating planewaves. The wavevector $k_x$ of these modes can be computed analytically: for a frequency of $\omega$ (in $c=1$ units), these propagating modes are the **real** solutions of $\sqrt{(\omega^2 n^2 - (k_y+2\pi m/\Lambda)^2)}$ where $m$ is the diffraction order (an integer), $\Lambda$ is the periodicity of the grating, and $n$ is the refractive index of the propagating medium. In this example, $n=1$, $k_y=0$, and $\Lambda=10$ μm. Thus, at a wavelength of 0.5 μm there are a total of 20 diffraction orders of which we only computed the first 10. The wavevector $k_x$ is used to compute the angle of the diffraction order as $\cos^{-1}(k_x/(\omega n))$. (The angle can also be equivalently computed as $\sin^{-1}((k_y+2\pi m/\Lambda)/(\omega n))$.) Evanescent modes, those with an imaginary $k_x$, exist for $|m|>20$ but these modes carry no power. Note that currently Meep does not compute the number of propagating modes for you. If the mode number passed to `get_eigenmode_coefficients` is larger than the number of propagating modes at a given frequency/wavelength, MPB's Newton solver will fail to converge and will return zero for the mode coefficient. It is therefore a good idea to know beforehand the number of propagating modes.


![](../images/grating_diffraction_spectra.png#center)



In the limit where the grating periodicity is much larger than the wavelength and the size of the diffracting element (i.e., more than 10 times), as it is in this example, the [diffraction efficiency](https://en.wikipedia.org/wiki/Diffraction_efficiency) can be computed analytically using scalar theory. This is described in the OpenCourseWare [Optics course](https://ocw.mit.edu/courses/mechanical-engineering/2-71-optics-spring-2009/) in the Lecture 16 (Gratings: Amplitude and Phase, Sinusoidal and Binary) [notes](https://ocw.mit.edu/courses/mechanical-engineering/2-71-optics-spring-2009/video-lectures/lecture-16-gratings-amplitude-and-phase-sinusoidal-and-binary/MIT2_71S09_lec16.pdf) and [video](https://www.youtube.com/watch?v=JmWguqCZRxk). For a review of scalar diffraction theory, see Chapter 3 ("Analysis of Two-Dimensional Signals and Systems") of [Introduction to Fourier Optics (fourth edition)](https://www.amazon.com/Introduction-Fourier-Optics-Joseph-Goodman-ebook/dp/B076TBP48F) by J.W. Goodman. From the scalar theory, the diffraction efficiency of the binary grating is $4/(m\pi)^2$ when the phase difference between the propagating distance in the glass relative to the same distance in air is $\pi$. The phase difference/contrast is $(2\pi/\lambda)(n-1)s$ where $\lambda$ is the wavelength, $n$ is the refractive index of the grating, and $s$ is the propagation distance in the grating (`gh` in the script). A special feature of the binary phase grating is that the diffraction efficiency is 0 for all *even* orders. This is verified by the diffraction spectrum shown above at $\lambda=0.5$ μm. Note the wavelength dependence of the transmittance and, in particular, the slightly *non-zero* diffraction efficiency for the even orders at wavelengths other than 0.5 μm. Since the diffraction efficiency of the ninth order has already fallen to a negligible value (~0.005), computing the spectra of higher-order modes is unnecessary.

To convert the diffraction efficiency into transmittance in the $x$ direction (in order to be able to compare the scalar-theory results with those from Meep), the diffraction efficiency must be multiplied by the Fresnel transmittance from air to glass and by the cosine of the diffraction angle. We compare the analytic and simulated results at a wavelength of 0.5 μm for diffraction orders 1 (2.9°), 3 (8.6°), 5 (14.5°), and 7 (20.5°). The analytic results are 0.3886, 0.0427, 0.0151, and 0.0074. The Meep results are 0.3891, 0.04287, 0.0152, and 0.0076. This corresponds to relative errors of approximately 1.3%, 0.4%, 0.8%, and 2.1% which indicates good agreement.

Finally, by investigating the transmittance of the zeroth order (at a wavelength of 0.5 μm) in the limit as the grating periodicity approaches zero, we can demonstrate the breakdown of the scalar theory in the wavelength-scale regime which can only be solved using a full-wave method. When the periodicity is much less than the wavelength (i.e., subwavelength), the transmittance can again be solved analytically using effective-medium theory involving a three-layer structure: a layer of the averaged $\varepsilon$ (mean or harmonic mean depending on the polarization $E_z$ or $H_z$) sandwiched between the glass substrate and air. Results are shown in the following figure.


![](../images/grating_0th_order_tran.png#center)



Starting around a grating periodicity of 1.0 μm, the transmittance is no longer zero and increases rapidly with decreasing periodicity. As shown in the inset, for periodicities less than 0.5 μm, the transmittance converges to its asymptotic limit determined by the effective-medium theory: 0.99744 for the $E_z$ and 0.99057 for the $H_z$ polarization. The weak polarization dependence is due to the low index contrast. The oscillations in the data are real and *not* an artifact of the discretization. For example, note the "hump" in the transmittance spectra for the $E_z$ polarization near a grating periodicity of 1.0 μm (twice the wavelength). This feature is associated with a "Wood anomaly" (see e.g. [Hessel and Oliner, 1965](https://www.osapublishing.org/ao/abstract.cfm?uri=ao-4-10-1275)), which occurs when new diffracted orders appear in the far field; for normal incidence, new diffraction orders appear as the period goes through any multiple of the wavelength.

### Reflectance and Transmittance Spectra for Planewave at Oblique Incidence

As an additional demonstration of the mode-decomposition feature, the reflectance and transmittance of all diffracted orders for any grating with no material absorption and a planewave source incident at any arbitrary angle and wavelength must necessarily sum to unity. Also, the total reflectance and transmittance must be equivalent to values computed using the Poynting flux. This demonstration is somewhat similar to the [single-mode waveguide example](#reflectance-of-a-waveguide-taper).

The following script is adapted from the previous binary-grating example involving a [normally-incident planewave](#transmittance-spectra-for-planewave-at-normal-incidence). The total reflectance, transmittance, and their sum are displayed at the end of the simulation on two separate lines prefixed by `mode-coeff:` and `poynting-flux:`.

Results are computed for a single wavelength of 0.5 μm. The pulsed planewave is incident at an angle of 10.7°. Its spatial profile is defined using the source amplitude function `pw_amp`. This [anonymous function](https://en.wikipedia.org/wiki/Anonymous_function) takes two arguments, the wavevector and a point in space (both `mp.Vector3`s), and returns a function of one argument which defines the planewave amplitude at that point. Even though we are computing the reflectance and transmittance at a single wavelength, the choice of the bandwidth of the pulsed source is important. This is because a broad-bandwidth source generates glancing-angle waves which are poorly absorbed by the PML (or by an absorber) which in turn prevents the simulation from terminating as the fields do not decay away. The solution is to use a narrow-bandwidth pulse which limits the generation of glancing-angle waves. Because launching glancing-angle waves is generally unavoidable, the `sim.run(until_after_sources=mp.stop_when_fields_decayed(...))` termination criteria is replaced with a fixed runtime via `sim.run(until_after_sources=200)`. As a general rule of thumb, the more oblique the planewave source, the longer the run time required to ensure accurate results. There is an additional line monitor between the source and the grating for computing the reflectance. The angle of each reflected/transmitted mode, which can be positive or negative, is computed using its dominant planewave vector. Since the oblique source breaks the symmetry in the $y$ direction, each diffracted order must be computed separately. In total, there are 59 reflected and 39 transmitted orders.

The simulation script is in [examples/binary_grating_oblique.py](https://github.com/NanoComp/meep/blob/master/python/examples/binary_grating_oblique.py). The notebook is [examples/binary_grating_oblique.ipynb](https://nbviewer.jupyter.org/github/NanoComp/meep/blob/master/python/examples/binary_grating_oblique.ipynb).

```py
import meep as mp
import math
import cmath
import numpy as np

resolution = 50        # pixels/μm

dpml = 1.0             # PML thickness
dsub = 3.0             # substrate thickness
dpad = 3.0             # length of padding between grating and PML
gp = 10.0              # grating period
gh = 0.5               # grating height
gdc = 0.5              # grating duty cycle

sx = dpml+dsub+gh+dpad+dpml
sy = gp

cell_size = mp.Vector3(sx,sy,0)
pml_layers = [mp.PML(thickness=dpml,direction=mp.X)]

wvl = 0.5              # center wavelength
fcen = 1/wvl           # center frequency
df = 0.05*fcen         # frequency width

ng = 1.5
glass = mp.Medium(index=ng)

use_cw_solver = False  # CW solver or time stepping?
tol = 1e-6             # CW solver tolerance
max_iters = 2000       # CW solver max iterations
L = 10                 # CW solver L

# rotation angle of incident planewave
# counter clockwise (CCW) about Z axis, 0 degrees along +X axis
theta_in = math.radians(10.7)

# k (in source medium) with correct length (plane of incidence: XY)
k = mp.Vector3(fcen*ng).rotate(mp.Vector3(z=1), theta_in)

symmetries = []
eig_parity = mp.ODD_Z
if theta_in == 0:
  k = mp.Vector3(0,0,0)
  symmetries = [mp.Mirror(mp.Y)]
  eig_parity += mp.EVEN_Y

def pw_amp(k,x0):
  def _pw_amp(x):
    return cmath.exp(1j*2*math.pi*k.dot(x+x0))
  return _pw_amp

src_pt = mp.Vector3(-0.5*sx+dpml+0.3*dsub,0,0)
sources = [mp.Source(mp.ContinuousSource(fcen,fwidth=df) if use_cw_solver else mp.GaussianSource(fcen,fwidth=df),
                     component=mp.Ez,
                     center=src_pt,
                     size=mp.Vector3(0,sy,0),
                     amp_func=pw_amp(k,src_pt))]

sim = mp.Simulation(resolution=resolution,
                    cell_size=cell_size,
                    boundary_layers=pml_layers,
                    k_point=k,
                    default_material=glass,
                    sources=sources,
                    symmetries=symmetries)

refl_pt = mp.Vector3(-0.5*sx+dpml+0.5*dsub,0,0)
refl_flux = sim.add_flux(fcen, 0, 1, mp.FluxRegion(center=refl_pt, size=mp.Vector3(0,sy,0)))

if use_cw_solver:
  sim.init_sim()
  sim.solve_cw(tol, max_iters, L)
else:
  sim.run(until_after_sources=100)

input_flux = mp.get_fluxes(refl_flux)
input_flux_data = sim.get_flux_data(refl_flux)

sim.reset_meep()

geometry = [mp.Block(material=glass,
                     size=mp.Vector3(dpml+dsub,mp.inf,mp.inf),
                     center=mp.Vector3(-0.5*sx+0.5*(dpml+dsub),0,0)),
            mp.Block(material=glass,
                     size=mp.Vector3(gh,gdc*gp,mp.inf),
                     center=mp.Vector3(-0.5*sx+dpml+dsub+0.5*gh,0,0))]

sim = mp.Simulation(resolution=resolution,
                    cell_size=cell_size,
                    boundary_layers=pml_layers,
                    geometry=geometry,
                    k_point=k,
                    sources=sources,
                    symmetries=symmetries)

refl_flux = sim.add_flux(fcen, 0, 1, mp.FluxRegion(center=refl_pt, size=mp.Vector3(0,sy,0)))
sim.load_minus_flux_data(refl_flux,input_flux_data)

tran_pt = mp.Vector3(0.5*sx-dpml-0.5*dpad,0,0)
tran_flux = sim.add_flux(fcen, 0, 1, mp.FluxRegion(center=tran_pt, size=mp.Vector3(0,sy,0)))

if use_cw_solver:
  sim.init_sim()
  sim.solve_cw(tol, max_iters, L)
else:
  sim.run(until_after_sources=200)

nm_r = np.floor((fcen*ng-k.y)*gp)-np.ceil((-fcen*ng-k.y)*gp) # number of reflected orders
if theta_in == 0:
  nm_r = nm_r/2 # since eig_parity removes degeneracy in y-direction
nm_r = int(nm_r)

res = sim.get_eigenmode_coefficients(refl_flux, range(1,nm_r+1), eig_parity=eig_parity)
r_coeffs = res.alpha

Rsum = 0
for nm in range(nm_r):
  r_kdom = res.kdom[nm]
  Rmode = abs(r_coeffs[nm,0,1])**2/input_flux[0]
  r_angle = np.sign(r_kdom.y)*math.acos(r_kdom.x/(ng*fcen))
  print("refl:, {:2d}, {:6.2f}, {:.8f}".format(nm,math.degrees(r_angle),Rmode))
  Rsum += Rmode

nm_t = np.floor((fcen-k.y)*gp)-np.ceil((-fcen-k.y)*gp)       # number of transmitted orders
if theta_in == 0:
  nm_t = nm_t/2 # since eig_parity removes degeneracy in y-direction
nm_t = int(nm_t)

res = sim.get_eigenmode_coefficients(tran_flux, range(1,nm_t+1), eig_parity=eig_parity)
t_coeffs = res.alpha

Tsum = 0
for nm in range(nm_t):
  t_kdom = res.kdom[nm]
  Tmode = abs(t_coeffs[nm,0,0])**2/input_flux[0]
  t_angle = np.sign(t_kdom.y)*math.acos(t_kdom.x/fcen)
  print("tran:, {:2d}, {:6.2f}, {:.8f}".format(nm,math.degrees(t_angle),Tmode))
  Tsum += Tmode

print("mode-coeff:, {:.6f}, {:11.6f}, {:.6f}".format(Rsum,Tsum,Rsum+Tsum))

r_flux = mp.get_fluxes(refl_flux)
t_flux = mp.get_fluxes(tran_flux)
Rflux = -r_flux[0]/input_flux[0]
Tflux =  t_flux[0]/input_flux[0]
print("poynting-flux:, {:.6f}, {:.6f}, {:.6f}".format(Rflux,Tflux,Rflux+Tflux))
```

Since this is a single-wavelength calculation, the [frequency-domain solver](../Python_User_Interface.md#frequency-domain-solver) can be used instead of time stepping for a possible performance enhancement. The only changes necessary to the original script are to replace two objects: (1) `GaussianSource` with `ContinuousSource` and (2) `run` with `solve_cw`. Choosing which approach to use is determined by the `use_cw_solver` boolean variable. In this example, mainly because of the oblique source, the frequency-domain solver converges slowly and is less efficient than the time-stepping simulation. The results from both approaches are nearly identical. Time stepping is therefore the default.

The following are several lines of output for eight of the reflected and transmitted orders. The first numerical column is the mode number, the second is the mode angle (in degrees), and the third is the fraction of the input power that is concentrated in the mode. Note that the thirteenth transmitted order at 19.18° contains nearly 38% of the input power.

```
...
refl:,  7,   6.83, 0.00006645
refl:,  8,  -8.49, 0.00005695
refl:,  9,   8.76, 0.00015756
refl:, 10, -10.43, 0.00001272
refl:, 11,  10.70, 0.04414669
refl:, 12, -12.38, 0.00005969
refl:, 13,  12.65, 0.00041535
refl:, 14, -14.34, 0.00001986
...
```

```
...
tran:, 12, -18.75, 0.00095438
tran:, 13,  19.18, 0.38260804
tran:, 14, -21.81, 0.00198524
tran:, 15,  22.24, 0.00107212
tran:, 16, -24.93, 0.00098416
tran:, 17,  25.37, 0.04148390
tran:, 18, -28.13, 0.00137340
tran:, 19,  28.59, 0.00113876
...
```

The mode number is equivalent to the band index from the MPB calculation. The ordering of the modes is according to *decreasing* values of $k_x$. The first mode has the largest $k_x$ and thus angle closest to 0°. As a corollary, the first mode has the smallest $|k_y+2\pi m/\lambda|$. For a non-zero $k_y$ (as in the case of an obliquely incident source), this expression will not necessarily be zero. The first seven reflected modes have $m$ values of -3, -4, -2, -5, -1, -6, and 0. These $m$ values are not monotonic. This is because $k_x$ is a nonlinear function of $m$ as shown earlier. The ordering of the transmitted modes is different since these modes are in vacuum and not glass (recall that the medium's refractive index is also a part of this nonlinear function). In the first example involving a normally incident source with $k_y = 0$, the ordering of the modes is monotonic: $m = 0, \pm 1, \pm 2, \dotsc$

The two main lines of the output are:

```
mode-coeff:,    0.061007, 0.937897, 0.998904
poynting-flux:, 0.061063, 0.938384, 0.999447
```

The first numerical column is the total reflectance, the second is the total transmittance, and the third is their sum. Results from the mode coefficients agree with the Poynting flux values to three decimal places. Also, the total reflectance and transmittance sum to unity. These results indicate that approximately 6% of the input power is reflected and the remaining 94% is transmitted.

### Diffracted Planewaves in Homogeneous Media

Rather than specify the diffracted planewave in homogeneous media using a band number (which is a property of the eigensolver), we can specify it directly using a [`DiffractedPlanewave`](../Python_User_Interface.md#diffractedplanewave). This is the only approach in 3d for specifying *non-degenerate* modes and is particularly useful when the incident planewave is oblique since in this case the band number does not directly relate to the diffraction order, as demonstrated previously. As diffracted planewaves are generally not mirror symmetric (because the grating itself is not symmetric or the planewave source is incident at an oblique angle), `DiffractedPlanewave` cannot take advantage of `symmetries` that bisect the monitor plane which means that it can only be used with `add_mode_monitor` rather than `add_flux`. A `DiffractedPlanewave` object can be passed as the `bands` argument of `get_eigenmode_coefficients` (or the `band_num` argument of `get_eigenmode`) and its constructor has four arguments: (1) a list/tuple of integers for the diffraction order, (2) a `Vector3` for the axis which together with the planewave's wavevector defines the "plane of incidence", and complex amplitudes for the (3) $\mathcal{S}$ and (4) $\mathcal{P}$ polarizations (i.e., electric field perpendicular or parallel to the plane of incidence, respectively). `DiffractedPlanewave` only computes *non-evanescent* propagating modes (i.e., the component of the wavevector in the non-periodic direction is real valued). For evanescent modes, a warning will be displayed and `get_eigenmode_coefficients` will return an empty object.

As a demonstration, the [previous example](#reflectance-and-transmittance-spectra-for-planewave-at-oblique-incidence) involving a binary grating with an input planewave at oblique incidence is modified such that the transmitted diffraction orders are computed using two different methods: (1) MPB's eigensolver and (2) `DiffractedPlanewave`. This example verifies that (1) both methods compute the same set of diffracted modes (although the ordering is different when the source is oblique) and (2) that the total power in all the orders is equivalent to the Poynting flux.

Shown below is the relevant section of the simulation involving the computation of the diffracted orders and their transmittance. The full simulation script is in [examples/diffracted_planewave.py](https://github.com/NanoComp/meep/blob/master/python/examples/diffracted_planewave.py).

```py
  # number of (non-evanescent) transmitted orders
  nm_t = np.floor((fcen-k.y)*gp)-np.ceil((-fcen-k.y)*gp)
  if theta_in == 0:
    nm_t = nm_t/2
  nm_t = int(nm_t)+1

  bands = range(1,nm_t+1)

  if theta_in == 0:
    orders = range(0,nm_t)
  else:
    orders = range(int(np.ceil((-fcen-k.y)*gp)),int(np.floor((fcen-k.y)*gp))+1)

  eig_sum = 0
  dp_sum = 0

  for band,order in zip(bands,orders):
    res = sim.get_eigenmode_coefficients(tran_mon, [band], eig_parity=eig_parity)
    if res is not None:
      tran_eig = abs(res.alpha[0,0,0])**2/input_flux[0]
      if theta_in == 0:
        tran_eig = 0.5*tran_eig
    else:
      tran_eig = 0
    eig_sum += tran_eig

    res = sim.get_eigenmode_coefficients(tran_mon,
                                         mp.DiffractedPlanewave((0,order,0),mp.Vector3(0,1,0),0,1))
    if res is not None:
      tran_dp = abs(res.alpha[0,0,0])**2/input_flux[0]
      if (theta_in == 0) and (order == 0):
        tran_dp = 0.5*tran_dp
    else:
      tran_dp = 0
    dp_sum += tran_dp

    if theta_in == 0:
      err = abs(tran_eig-tran_dp)/tran_eig
      print("tran:, {:2d}, {:.8f}, {:2d}, {:.8f}, {:.8f}".format(band,tran_eig,order,tran_dp,err))
    else:
      print("tran:, {:2d}, {:.8f}, {:2d}, {:.8f}".format(band,tran_eig,order,tran_dp))

  flux = mp.get_fluxes(tran_mon)
  t_flux = flux[0]/input_flux[0]
  if (theta_in == 0):
    t_flux = 0.5*t_flux

  err = abs(dp_sum-t_flux)/t_flux
  print("flux:, {:.8f}, {:.8f}, {:.8f}, {:.8f}".format(eig_sum,
                                                       dp_sum,
                                                       t_flux,
                                                       err))
```

There are four items to note regarding the use of `DiffractedPlanewave`: (1) the diffraction order `(0,order,0)` contains non-zero elements for only the $d-1$ periodic directions of the $d$ dimensional cell (which is just the $y$ direction in this example), (2) specifying properties of the eigensolver including `eig_parity`, `eig_resolution`, `eig_tolerance`, and `kpoint_func` as part of the call to `get_eigenmode_coefficients` is not necessary (and is ignored), (3) in 2d, the `axis` is chosen as `Vector3(0,1,0)` (the direction parallel to the source) although *any* vector in the $xy$ plane that is not parallel to the mode's wavevector is also valid, and (4) since the source has $H_z$ polarization (not shown), the $\mathcal{S}$ polarization amplitude is 0 and the $\mathcal{P}$ polarization is 1.

Results of this calculation are shown below for two different grating configurations:

1. `gp`=2.6 μm, `gh`=0.4 μm, `gdc`=0.3 μm, incident angle of 0°
2. `gp`=3.7 μm, `gh`=0.6 μm, `gdc`=0.4 μm, incident angle of 13.5°

In the first configuration, the output on each line prefixed by `tran:,` consists of five values: the band index, transmittance of the diffracted planewave obtained using the eigensolver, the diffraction order, transmittance of the diffracted planewave obtained using `DiffractedPlanewave`, and relative error of the transmittance. As can be seen by the transmittance values on each line, there is a direct relationship between the band number and the diffraction order (i.e., band number 1 corresponds to diffraction order 0, band number 2 with diffraction order 1, etc.) because the input planewave is normally incident. The last line prefixed by `flux:,` lists the total power obtained using the eigensolver, `DiffractedPlanewave`, Poynting flux, and relative error of the `DiffractedPlanewave` result with respect to the Poynting flux.

```
tran:,  1, 0.12695973,  0, 0.12696027, 0.00000428
tran:,  2, 0.24552342,  1, 0.24552348, 0.00000025
tran:,  3, 0.07401465,  2, 0.07401465, 0.00000002
tran:,  4, 0.00793261,  3, 0.00793262, 0.00000078
tran:,  5, 0.01094389,  4, 0.01094389, 0.00000010
tran:,  6, 0.01361924,  5, 0.01362885, 0.00070525

flux:, 0.47899353, 0.47900375, 0.47898568, 0.00003772
```

In the second configuration, the output is similar to the first configuration with the only difference being the lines prefixed by `tran:,` do not include the relative error as the final column. Whereas in the first configuration the transmittance for the two methods is nearly equivalent on each line, this is not the case in the second configuration since the incident planewave is oblique. Although the order of the diffracted modes is different (i.e., band number 1 corresponds to diffraction order $m=-3$, band number 2 with diffraction order $m=-2$, band number 3 with $m=-4$, etc.), the total power in all the modes is equivalent for all three methods.

```
tran:,  1, 0.02879456, -9, 0.00594139
tran:,  2, 0.02505013, -8, 0.00615678
tran:,  3, 0.01737490, -7, 0.00709585
tran:,  4, 0.32428997, -6, 0.01121764
tran:,  5, 0.00957856, -5, 0.00957870
tran:,  6, 0.09070071, -4, 0.01737485
tran:,  7, 0.01121627, -3, 0.02879462
tran:,  8, 0.29570513, -2, 0.02505018
tran:,  9, 0.00709584, -1, 0.32429003
tran:, 10, 0.03461314,  0, 0.09070063
tran:, 11, 0.00615701,  1, 0.29570530
tran:, 12, 0.02832782,  2, 0.03461314
tran:, 13, 0.00594127,  3, 0.02832783
tran:, 14, 0.02346054,  4, 0.0234605

flux:, 0.90830587, 0.90830748, 0.90911585, 0.00088919
```

Diffracted Orders of a Triangular/Hexagonal Lattice
---------------------------------------------------

While it is straightforward to compute the diffracted orders of a square lattice, a triangular/hexagonal lattice requires some care. This is because Meep only supports a rectilinear cell lattice. It is therefore not possible to directly simulate the unit cell of a triangular lattice. The workaround is to use a (rectilinear) *supercell* but then the diffracted orders must be defined differently in order to correspond exactly to those of the actual unit cell. This is because the supercell introduces artificial diffraction orders (forbidden by the higher symmetry of the underlying triangular lattice) that carry no power. As a demonstration, we will compute the transmitted orders of a 2D grating with triangular lattice. We will verify that only the "real" orders contain nonzero power whereas the artificial ones contain zero power.

As shown in the left side of the figure below, the lattice vectors of a triangular lattice are $\vec{a_1} = (\Lambda,0)$ and $\vec{a_2}=(\frac{\Lambda}{2},\frac{\sqrt{3}}{2}\Lambda)$ where $\Lambda$ is the lattice periodicity. The unit cell is marked by the dotted silver line. The [reciprocal lattice vectors](https://en.wikipedia.org/wiki/Reciprocal_lattice#Two_dimensions) are $\vec{b_1}=\frac{2\pi}{\Lambda}(1,-1/\sqrt{3})$ and $\vec{b_2}=\frac{2\pi}{\Lambda}(0,2/\sqrt{3})$. An in-plane ($xy$) diffracted order of the unit cell can be defined as $\vec{k_\parallel}=m_1\vec{b_1}+m_2\vec{b_2}$ where $m_1$ and $m_2$ are integers.

For the supercell shown in the right side of the figure, the lattice vectors are $\vec{a_1} = (\Lambda,0)$ and $\vec{a_3} = (0,\sqrt{3}\Lambda)$. Its reciprocal lattice vectors are $\vec{b'_1}=\frac{2\pi}{\Lambda}(1,0)$ and $\vec{b'_2}=\frac{2\pi}{\Lambda}(0,1/\sqrt{3})$. Note that the dot product of $\vec{b'_1}$ and $\vec{b'_2}$ is zero because they are orthogonal. An in-plane diffracted order of the supercell can be defined as $\vec{k_{SC}}=n_1\vec{b'_1}+n_2\vec{b'_2}$ where $n_1$ and $n_2$ are integers.

Given a "real" diffracted order specified by $(m_1,m_2)$, we need to determine the equivalent order of the supercell specified by $(n_1,n_2)$ for use in the simulation when computing the mode coefficients. Setting $\vec{k_{SC}}=\vec{k_\parallel}$ and solving for the pair of equations yields: $n_1=m_1$ and $n_2=-m_1+2m_2$.


![](../images/triangular_lattice.png#center)


To demonstrate this in practice, we will compute the power (an absolute quantity) of the $(0,1)$ order of a triangular lattice of cylindrical rods (height: 0.5 µm, radius: 0.1 µm) on a glass ($n=1.5$) substrate with periodicity of 1.0 µm. Note that this is a 3D simulation. In this example, the plane of incidence is $yz$ and the $E_x$ source therefore corresponds to the $\mathcal{S}$ polarization.

The simulation script is in [examples/grating2d_triangular_lattice.py](https://github.com/NanoComp/meep/blob/master/python/examples/grating2d_triangular_lattice.py).

```py
import meep as mp
import math
import numpy as np

resolution = 100  # pixels/μm

ng = 1.5
glass = mp.Medium(index=ng)

wvl = 0.5  # wavelength
fcen = 1/wvl

# rectangular supercell
sx = 1.0
sy = np.sqrt(3)

dpml = 1.0  # PML thickness
dsub = 2.0  # substrate thickness
dair = 2.0  # air padding
hcyl = 0.5  # cylinder height
rcyl = 0.1  # cylinder radius

sz = dpml+dsub+hcyl+dair+dpml

cell_size = mp.Vector3(sx,sy,sz)

boundary_layers = [mp.PML(thickness=dpml,direction=mp.Z)]

# periodic boundary conditions
k_point = mp.Vector3()

src_pt = mp.Vector3(0,0,-0.5*sz+dpml)
sources = [mp.Source(src=mp.GaussianSource(fcen,fwidth=0.1*fcen),
                     size=mp.Vector3(sx,sy,0),
                     center=src_pt,
                     component=mp.Ex)]

substrate = [mp.Block(size=mp.Vector3(mp.inf,mp.inf,dpml+dsub),
                      center=mp.Vector3(0,0,-0.5*sz+0.5*(dpml+dsub)),
                      material=glass)]

cyl_grating = [mp.Cylinder(center=mp.Vector3(0,0,-0.5*sz+dpml+dsub+0.5*hcyl),
                           radius=rcyl,
                           height=hcyl,
                           material=glass),
               mp.Cylinder(center=mp.Vector3(0.5*sx,0.5*sy,-0.5*sz+dpml+dsub+0.5*hcyl),
                           radius=rcyl,
                           height=hcyl,
                           material=glass),
               mp.Cylinder(center=mp.Vector3(-0.5*sx,0.5*sy,-0.5*sz+dpml+dsub+0.5*hcyl),
                           radius=rcyl,
                           height=hcyl,
                           material=glass),
               mp.Cylinder(center=mp.Vector3(-0.5*sx,-0.5*sy,-0.5*sz+dpml+dsub+0.5*hcyl),
                           radius=rcyl,
                           height=hcyl,
                           material=glass),
               mp.Cylinder(center=mp.Vector3(0.5*sx,-0.5*sy,-0.5*sz+dpml+dsub+0.5*hcyl),
                           radius=rcyl,
                           height=hcyl,
                           material=glass)]

geometry = substrate + cyl_grating

sim = mp.Simulation(resolution=resolution,
                    cell_size=cell_size,
                    sources=sources,
                    geometry=geometry,
                    boundary_layers=boundary_layers,
                    k_point=k_point)

tran_pt = mp.Vector3(0,0,0.5*sz-dpml)
tran_flux = sim.add_mode_monitor(fcen,
                                 0,
                                 1,
                                 mp.ModeRegion(center=tran_pt,
                                               size=mp.Vector3(sx,sy,0)))

sim.run(until_after_sources=mp.stop_when_fields_decayed(20,mp.Ex,src_pt,1e-6))

# unit cell (triangular lattice)
mx = 0  # diffraction order in x direction
my = 1  # diffraction order in y direction

# check: for diffraction orders of supercell for which
#        nx = mx and ny = -mx + 2*my and thus
#        only even orders should produce nonzero power
nx = mx
for ny in range(4):
    kz2 = fcen**2-(nx/sx)**2-(ny/sy)**2
    if kz2 > 0:
        res = sim.get_eigenmode_coefficients(tran_flux,
                                             mp.DiffractedPlanewave((nx,ny,0),
                                                                    mp.Vector3(0,1,0),
                                                                    1,
                                                                    0))
        t_coeffs = res.alpha
        tran = abs(t_coeffs[0,0,0])**2

        print("order:, {}, {}, {:.5f}".format(nx,ny,tran))
```

The output lists the power in the orders labeled by $n_1$ and $n_2$. Because $n_1=m_1$ and $n_2=-m_1+2m_2$, only those supercell orders with even $n_2$ contain nonzero power whereas the odd orders (artifacts of the supercell) contain zero power. Note that the $(m_1,m_2)=(0,1)$ order of the unit cell corresponds to the $(n_1,n_2)=(0,2)$ order of the supercell.

```
order:, 0, 0, 1.46914
order:, 0, 1, 0.00000
order:, 0, 2, 0.03570
order:, 0, 3, 0.00000
```


Phase Map of a Subwavelength Binary Grating
-------------------------------------------

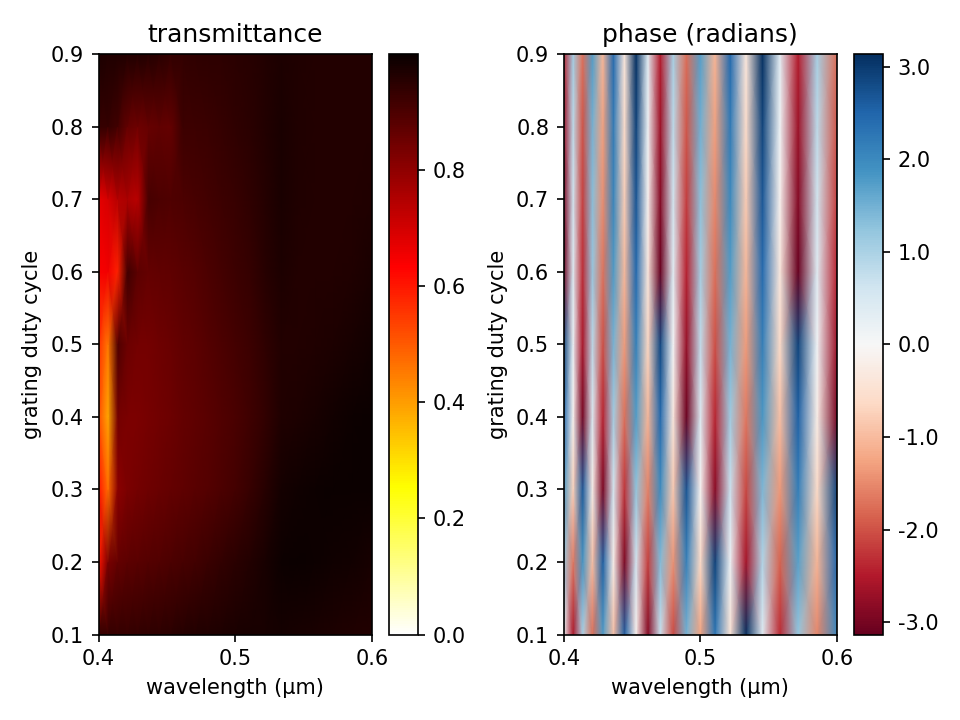
We can also use the complex mode coefficients to compute the phase (or impedance) of the diffraction orders. This can be used to generate a phase map of the binary grating as a function of its geometric parameters. Phase maps are important for the design of subwavelength phase shifters such as those used in a metasurface lens. When the period of the unit cell is subwavelength, the zeroth-diffraction order is the only propagating wave. In this demonstration, which is adapted from the previous example, we compute the transmittance spectra and phase map of the zeroth-diffraction order (at 0°) for an $E_z$-polarized planewave pulse spanning wavelengths of 0.4 to 0.6 μm which is normally incident on a binary grating with a periodicity of 0.35 μm and height of 0.6 μm. The duty cycle of the grating is varied from 0.1 to 0.9 in separate runs.

The simulation script is in [examples/binary_grating_phasemap.py](https://github.com/NanoComp/meep/blob/master/python/examples/binary_grating_phasemap.py). The notebook is [examples/binary_grating_phasemap.ipynb](https://nbviewer.jupyter.org/github/NanoComp/meep/blob/master/python/examples/binary_grating_phasemap.ipynb).

```py
import meep as mp
import numpy as np
import matplotlib.pyplot as plt
import numpy.matlib
import argparse

resolution = 60         # pixels/μm

dpml = 1.0              # PML thickness
dsub = 3.0              # substrate thickness
dpad = 3.0              # padding between grating and PML

wvl_min = 0.4           # min wavelength
wvl_max = 0.6           # max wavelength
fmin = 1/wvl_max        # min frequency
fmax = 1/wvl_min        # max frequency
fcen = 0.5*(fmin+fmax)  # center frequency
df = fmax-fmin          # frequency width
nfreq = 21              # number of frequency bins

k_point = mp.Vector3(0,0,0)

glass = mp.Medium(index=1.5)

def grating(gp,gh,gdc,oddz):
  sx = dpml+dsub+gh+dpad+dpml
  sy = gp

  cell_size = mp.Vector3(sx,sy,0)
  pml_layers = [mp.PML(thickness=dpml,direction=mp.X)]

  src_pt = mp.Vector3(-0.5*sx+dpml+0.5*dsub,0,0)
  sources = [mp.Source(mp.GaussianSource(fcen, fwidth=df), component=mp.Ez if oddz else mp.Hz, center=src_pt, size=mp.Vector3(0,sy,0))]

  symmetries=[mp.Mirror(mp.Y, phase=+1 if oddz else -1)]

  sim = mp.Simulation(resolution=resolution,
                      cell_size=cell_size,
                      boundary_layers=pml_layers,
                      k_point=k_point,
                      default_material=glass,
                      sources=sources,
                      symmetries=symmetries)

  mon_pt = mp.Vector3(0.5*sx-dpml-0.5*dpad,0,0)
  flux_mon = sim.add_flux(fcen, df, nfreq, mp.FluxRegion(center=mon_pt, size=mp.Vector3(0,sy,0)))

  sim.run(until_after_sources=100)

  input_flux = mp.get_fluxes(flux_mon)

  sim.reset_meep()

  geometry = [mp.Block(material=glass, size=mp.Vector3(dpml+dsub,mp.inf,mp.inf), center=mp.Vector3(-0.5*sx+0.5*(dpml+dsub),0,0)),
              mp.Block(material=glass, size=mp.Vector3(gh,gdc*gp,mp.inf), center=mp.Vector3(-0.5*sx+dpml+dsub+0.5*gh,0,0))]

  sim = mp.Simulation(resolution=resolution,
                      cell_size=cell_size,
                      boundary_layers=pml_layers,
                      geometry=geometry,
                      k_point=k_point,
                      sources=sources,
                      symmetries=symmetries)

  mode_mon = sim.add_flux(fcen, df, nfreq, mp.FluxRegion(center=mon_pt, size=mp.Vector3(0,sy,0)))

  sim.run(until_after_sources=300)

  freqs = mp.get_eigenmode_freqs(mode_mon)
  res = sim.get_eigenmode_coefficients(mode_mon, [1], eig_parity=mp.ODD_Z+mp.EVEN_Y if oddz else mp.EVEN_Z+mp.ODD_Y)
  coeffs = res.alpha

  mode_wvl = [1/freqs[nf] for nf in range(nfreq)]
  mode_tran = [abs(coeffs[0,nf,0])**2/input_flux[nf] for nf in range(nfreq)]
  mode_phase = [np.angle(coeffs[0,nf,0]) for nf in range(nfreq)]

  return mode_wvl, mode_tran, mode_phase

if __name__ == '__main__':
  parser = argparse.ArgumentParser()
  parser.add_argument('-gp', type=float, default=0.35, help='grating periodicity (default: 0.35 μm)')
  parser.add_argument('-gh', type=float, default=0.6, help='grating height (default: 0.6 μm)')
  parser.add_argument('-oddz', action='store_true', default=False, help='oddz? (default: False)')
  args = parser.parse_args()

  gdc = np.arange(0.1,1.0,0.1)
  mode_tran = np.empty((gdc.size,nfreq))
  mode_phase = np.empty((gdc.size,nfreq))
  for n in range(gdc.size):
    mode_wvl, mode_tran[n,:], mode_phase[n,:] = grating(args.gp,args.gh,gdc[n],args.oddz)

  plt.figure(dpi=150)

  plt.subplot(1,2,1)
  plt.pcolormesh(mode_wvl, gdc, mode_tran, cmap='hot_r', shading='gouraud', vmin=0, vmax=mode_tran.max())
  plt.axis([wvl_min, wvl_max, gdc[0], gdc[-1]])
  plt.xlabel("wavelength (μm)")
  plt.xticks([t for t in np.arange(wvl_min,wvl_max+0.1,0.1)])
  plt.ylabel("grating duty cycle")
  plt.yticks([t for t in np.arange(gdc[0],gdc[-1]+0.1,0.1)])
  plt.title("transmittance")
  cbar = plt.colorbar()
  cbar.set_ticks([t for t in np.arange(0,1.2,0.2)])
  cbar.set_ticklabels(["{:.1f}".format(t) for t in np.arange(0,1.2,0.2)])

  plt.subplot(1,2,2)
  plt.pcolormesh(mode_wvl, gdc, mode_phase, cmap='RdBu', shading='gouraud', vmin=mode_phase.min(), vmax=mode_phase.max())
  plt.axis([wvl_min, wvl_max, gdc[0], gdc[-1]])
  plt.xlabel("wavelength (μm)")
  plt.xticks([t for t in np.arange(wvl_min,wvl_max+0.1,0.1)])
  plt.ylabel("grating duty cycle")
  plt.yticks([t for t in np.arange(gdc[0],gdc[-1]+0.1,0.1)])
  plt.title("phase (radians)")
  cbar = plt.colorbar()
  cbar.set_ticks([t for t in range(-3,4)])
  cbar.set_ticklabels(["{:.1f}".format(t) for t in range(-3,4)])

  plt.tight_layout()
  plt.show()
```

The phase of the zeroth-diffraction order is simply the angle of its complex mode coefficient. Note that it is generally only the relative phase (the phase difference) between different structures that is useful. The overall mode coefficient $\alpha$ is multiplied by a complex number given by the source amplitude, as well as an arbitrary (but deterministic) phase choice by the mode solver MPB (i.e., which maximizes the energy in the real part of the fields via [`ModeSolver.fix_field_phase`](https://mpb.readthedocs.io/en/latest/Python_User_Interface/#loading-and-manipulating-the-current-field)) — but as long as you keep the current source fixed as you vary the parameters of the structure, the relative phases are meaningful.

The script is run from the shell terminal using: `python binary_grating_phasemap.py -gp 0.35 -gh 0.6 -oddz`. The figure below shows the transmittance spectra (left) and phase map (right). The transmittance is nearly unity over most of the parameter space mainly because of the subwavelength dimensions of the grating. The phase variation spans the full range of $-\pi$ to $+\pi$ at each wavelength but varies weakly with the duty cycle due to the relatively low index of the glass grating. Higher-index materials such as [titanium dioxide](https://en.wikipedia.org/wiki/Titanium_dioxide#Thin_films) (TiO<sub>2</sub>) generally provide more control over the phase.


![](../images/grating_phasemap.png#center)



See [Tutorials/Near to Far Field Spectra/Focusing Properties of a Metasurface Lens](Near_to_Far_Field_Spectra.md#focusing-properties-of-a-metasurface-lens) for a related example.

Diffraction Spectrum of Liquid-Crystal Polarization Gratings
------------------------------------------------------------

As a final demonstration of mode decomposition, we compute the diffraction spectrum of a [liquid-crystal](https://en.wikipedia.org/wiki/Liquid_crystal) polarization grating. These types of beam splitters use [birefringence](https://en.wikipedia.org/wiki/Birefringence) to produce diffraction orders which are [circularly polarized](https://en.wikipedia.org/wiki/Circular_polarization). We will investigate two kinds of polarization gratings: (1) a homogeneous [uniaxial](https://en.wikipedia.org/wiki/Birefringence#Uniaxial_materials) grating (commonly known as a circular-polarization grating), and (2) a [twisted-nematic](https://en.wikipedia.org/wiki/Liquid_crystal#Chiral_phases) bilayer grating as described in [Optics Letters, Vol. 33, No. 20, pp. 2287-9 (2008)](https://www.osapublishing.org/ol/abstract.cfm?uri=ol-33-20-2287) ([pdf](https://www.imagineoptix.com/cms/wp-content/uploads/2017/01/OL_08_Oh-broadband_PG.pdf)). The homogeneous uniaxial grating is just a special case of the twisted-nematic grating with a nematic [director](https://en.wikipedia.org/wiki/Liquid_crystal#Director) rotation angle of $\phi=0^{\circ}$.

A schematic of the grating geometry is shown below. The grating is a 2d slab in the $xy$-plane with two parameters: birefringence ($\Delta n$) and thickness ($d$). The twisted-nematic grating consists of two layers of thickness $d$ each with equal and opposite rotation angles of $\phi = 70^{\circ}$ for the nematic director. Both gratings contain only three diffraction orders: $m = 0, \pm 1$. The $m=0$ order is linearly polarized and the $m=\pm 1$ orders are circularly polarized with opposite chirality. For the uniaxial grating, the diffraction efficiencies for a mode with wavelength $\lambda$ can be computed analytically: $\eta_0 = \cos^2(\pi\Delta n d/\lambda)$, $\eta_{\pm 1} = 0.5\sin^2(\pi\Delta n d/\lambda)$. The derivation of these formulas is presented in [Optics Letters, Vol. 24, No. 9, pp. 584-6 (1999)](https://www.osapublishing.org/ol/abstract.cfm?uri=ol-24-9-584). We will verify these analytic results and also demonstrate that the twisted-nematic grating produces a broader bandwidth response for the ±1 orders than the homogeneous uniaxial grating. An important property of these polarization gratings for e.g. display applications is that for a circular-polarized input planewave and phase delay ($\Delta n d/\lambda$) of nearly 0.5, there is only a single diffraction order (+1 or -1) with *opposite* chiraity to that of the input. This is also demonstrated below.


![](../images/polarization_grating_schematic.png#center)



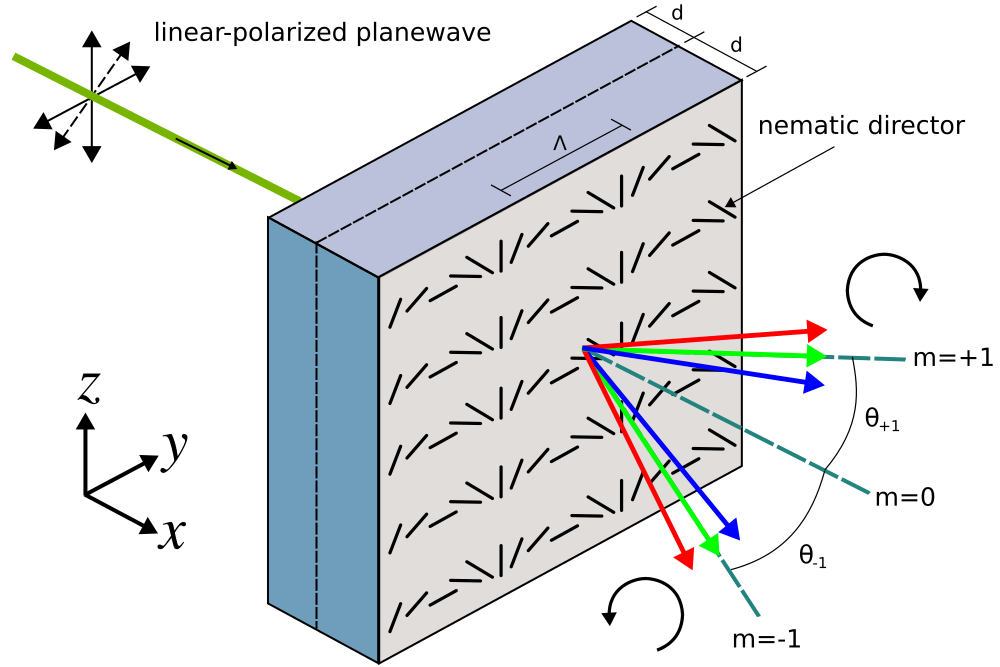
In this example, the input is a linear-polarized planewave pulse at normal incidence with center wavelength of $\lambda = 0.54$ μm. The linear polarization is in the $yz$-plane with a rotation angle of 45° counter clockwise around the $x$ axis. Two sets of mode coefficients are computed in the air region adjacent to the grating for each orthogonal polarization: `ODD_Z+EVEN_Y` and `EVEN_Z+ODD_Y`, which correspond to $+k_y + -k_y$ (cosine) and $+k_y - -k_y$ (sine) modes. From these coefficients for linear-polarized modes, the power in the circular-polarized modes can be computed: |ODD_Z+EVEN_Y|<sup>2</sup>+|EVEN_Z+ODD_Y|<sup>2</sup>. The power is identical for the two circular-polarized modes with opposite chiralities since the input is linearly polarized and at normal incidence. The transmittance for the diffraction orders are computed from the mode coefficients. Following usual practice, this requires a separate normalization run to compute the power of the input planewave.

The simulation script is in [examples/polarization_grating.py](https://github.com/NanoComp/meep/blob/master/python/examples/polarization_grating.py). The notebook is [examples/polarization_grating.ipynb](https://nbviewer.jupyter.org/github/NanoComp/meep/blob/master/python/examples/polarization_grating.ipynb).

The main part of the script is the function `pol_grating` which computes the mode coefficients for a grating with thickness `d`, twisted-nematic rotation angle `ph`, and periodicity `gp`. The anisotropic permittivity of the grating is specified using the [material function](../Python_User_Interface.md#medium) `lc_mat` which involves a position-dependent rotation of the diagonal $\varepsilon$ tensor about the $x$-axis. For $\phi = 0^{\circ}$, the nematic director is oriented along the $z$-axis: $E_z$ has a larger permittivity than $E_y$ where the birefringence ($\Delta n$) is 0.159. The grating has a periodicity of $\Lambda = 6.5$ μm in the $y$ direction.

```py
import meep as mp
import numpy as np
import math
import matplotlib.pyplot as plt

resolution = 50        # pixels/μm

dpml = 1.0             # PML thickness
dsub = 1.0             # substrate thickness
dpad = 1.0             # padding thickness

k_point = mp.Vector3(0,0,0)

pml_layers = [mp.PML(thickness=dpml,direction=mp.X)]

n_0 = 1.55
delta_n = 0.159
epsilon_diag = mp.Matrix(mp.Vector3(n_0**2,0,0),mp.Vector3(0,n_0**2,0),mp.Vector3(0,0,(n_0+delta_n)**2))

wvl = 0.54             # center wavelength
fcen = 1/wvl           # center frequency

def pol_grating(d,ph,gp,nmode):
    sx = dpml+dsub+d+d+dpad+dpml
    sy = gp

    cell_size = mp.Vector3(sx,sy,0)

    # twist angle of nematic director; from equation 1b
    def phi(p):
        xx  = p.x-(-0.5*sx+dpml+dsub)
        if (xx >= 0) and (xx <= d):
            return math.pi*p.y/gp + ph*xx/d
        else:
            return math.pi*p.y/gp - ph*xx/d + 2*ph

    # return the anisotropic permittivity tensor for a uniaxial, twisted nematic liquid crystal
    def lc_mat(p):
        # rotation matrix for rotation around x axis
        Rx = mp.Matrix(mp.Vector3(1,0,0),mp.Vector3(0,math.cos(phi(p)),math.sin(phi(p))),mp.Vector3(0,-math.sin(phi(p)),math.cos(phi(p))))
        lc_epsilon = Rx * epsilon_diag * Rx.transpose()
        lc_epsilon_diag = mp.Vector3(lc_epsilon[0].x,lc_epsilon[1].y,lc_epsilon[2].z)
        lc_epsilon_offdiag = mp.Vector3(lc_epsilon[1].x,lc_epsilon[2].x,lc_epsilon[2].y)
        return mp.Medium(epsilon_diag=lc_epsilon_diag,epsilon_offdiag=lc_epsilon_offdiag)

    geometry = [mp.Block(center=mp.Vector3(-0.5*sx+0.5*(dpml+dsub)),size=mp.Vector3(dpml+dsub,mp.inf,mp.inf),material=mp.Medium(index=n_0)),
                mp.Block(center=mp.Vector3(-0.5*sx+dpml+dsub+d),size=mp.Vector3(2*d,mp.inf,mp.inf),material=lc_mat)]

    # linear-polarized planewave pulse source
    src_pt = mp.Vector3(-0.5*sx+dpml+0.3*dsub,0,0)
    sources = [mp.Source(mp.GaussianSource(fcen,fwidth=0.05*fcen), component=mp.Ez, center=src_pt, size=mp.Vector3(0,sy,0)),
               mp.Source(mp.GaussianSource(fcen,fwidth=0.05*fcen), component=mp.Ey, center=src_pt, size=mp.Vector3(0,sy,0))]

    sim = mp.Simulation(resolution=resolution,
                        cell_size=cell_size,
                        boundary_layers=pml_layers,
                        k_point=k_point,
                        sources=sources,
                        default_material=mp.Medium(index=n_0))

    tran_pt = mp.Vector3(0.5*sx-dpml-0.5*dpad,0,0)
    tran_flux = sim.add_flux(fcen, 0, 1, mp.FluxRegion(center=tran_pt, size=mp.Vector3(0,sy,0)))

    sim.run(until_after_sources=100)

    input_flux = mp.get_fluxes(tran_flux)

    sim.reset_meep()

    sim = mp.Simulation(resolution=resolution,
                        cell_size=cell_size,
                        boundary_layers=pml_layers,
                        k_point=k_point,
                        sources=sources,
                        geometry=geometry)

    tran_flux = sim.add_flux(fcen, 0, 1, mp.FluxRegion(center=tran_pt, size=mp.Vector3(0,sy,0)))

    sim.run(until_after_sources=300)

    res1 = sim.get_eigenmode_coefficients(tran_flux, range(1,nmode+1), eig_parity=mp.ODD_Z+mp.EVEN_Y)
    res2 = sim.get_eigenmode_coefficients(tran_flux, range(1,nmode+1), eig_parity=mp.EVEN_Z+mp.ODD_Y)
    angles = [math.degrees(math.acos(kdom.x/fcen)) for kdom in res1.kdom]

    return input_flux[0], angles, res1.alpha[:,0,0], res2.alpha[:,0,0];
```

The properties of the two gratings are computed over a range of thicknesses from 0.1 to 3.4 μm corresponding to phase delays ($\Delta n d/\lambda$) of approximately 0 to 1.

```py
ph_uniaxial = 0               # chiral layer twist angle for uniaxial grating
ph_twisted = 70               # chiral layer twist angle for bilayer grating
gp = 6.5                      # grating period
nmode = 5                     # number of mode coefficients to compute
dd = np.arange(0.1,3.5,0.1)   # chiral layer thickness

m0_uniaxial = np.zeros(dd.size)
m1_uniaxial = np.zeros(dd.size)
ang_uniaxial = np.zeros(dd.size)

m0_twisted = np.zeros(dd.size)
m1_twisted = np.zeros(dd.size)
ang_twisted = np.zeros(dd.size)

for k in range(len(dd)):
    input_flux, angles, coeffs1, coeffs2 = pol_grating(0.5*dd[k],math.radians(ph_uniaxial),gp,nmode)
    tran = (abs(coeffs1)**2+abs(coeffs2)**2)/input_flux
    for m in range(nmode):
        print("tran (uniaxial):, {}, {:.2f}, {:.5f}".format(m,angles[m],tran[m]))
    m0_uniaxial[k] = tran[0]
    m1_uniaxial[k] = tran[1]
    ang_uniaxial[k] = angles[1]

    input_flux, angles, coeffs1, coeffs2 = pol_grating(dd[k],math.radians(ph_twisted),gp,nmode)
    tran = (abs(coeffs1)**2+abs(coeffs2)**2)/input_flux
    for m in range(nmode):
        print("tran (twisted):, {}, {:.2f}, {:.5f}".format(m,angles[m],tran[m]))
    m0_twisted[k] = tran[0]
    m1_twisted[k] = tran[1]
    ang_twisted[k] = angles[1]
```

The diffraction spectra is plotted using the script below and shown in the accompanying figure.

```py
cos_angles = [math.cos(math.radians(t)) for t in ang_uniaxial]
tran = m0_uniaxial+2*m1_uniaxial
eff_m0 = m0_uniaxial/tran
eff_m1 = (2*m1_uniaxial/tran)/cos_angles

phase = delta_n*dd/wvl
eff_m0_analytic = [math.cos(math.pi*p)**2 for p in phase]
eff_m1_analytic = [math.sin(math.pi*p)**2 for p in phase]

plt.figure(dpi=150)
plt.subplot(1,2,1)
plt.plot(phase,eff_m0,'bo-',clip_on=False,label='0th order (meep)')
plt.plot(phase,eff_m0_analytic,'b--',clip_on=False,label='0th order (analytic)')
plt.plot(phase,eff_m1,'ro-',clip_on=False,label='±1 orders (meep)')
plt.plot(phase,eff_m1_analytic,'r--',clip_on=False,label='±1 orders (analytic)')
plt.axis([0, 1.0, 0, 1])
plt.xticks([t for t in np.arange(0,1.2,0.2)])
plt.xlabel("phase delay Δnd/λ")
plt.ylabel("diffraction efficiency @ λ = 0.54 μm")
plt.legend(loc='center')
plt.title("homogeneous uniaxial grating")

cos_angles = [math.cos(math.radians(t)) for t in ang_twisted]
tran = m0_twisted+2*m1_twisted
eff_m0 = m0_twisted/tran
eff_m1 = (2*m1_twisted/tran)/cos_angles

plt.subplot(1,2,2)
plt.plot(phase,eff_m0,'bo-',clip_on=False,label='0th order (meep)')
plt.plot(phase,eff_m1,'ro-',clip_on=False,label='±1 orders (meep)')
plt.axis([0, 1.0, 0, 1])
plt.xticks([t for t in np.arange(0,1.2,0.2)])
plt.xlabel("phase delay Δnd/λ")
plt.ylabel("diffraction efficiency @ λ = 0.54 μm")
plt.legend(loc='center')
plt.title("bilayer twisted-nematic grating")

plt.show()
```

![](../images/polarization_grating_diffraction_spectra.png#center)


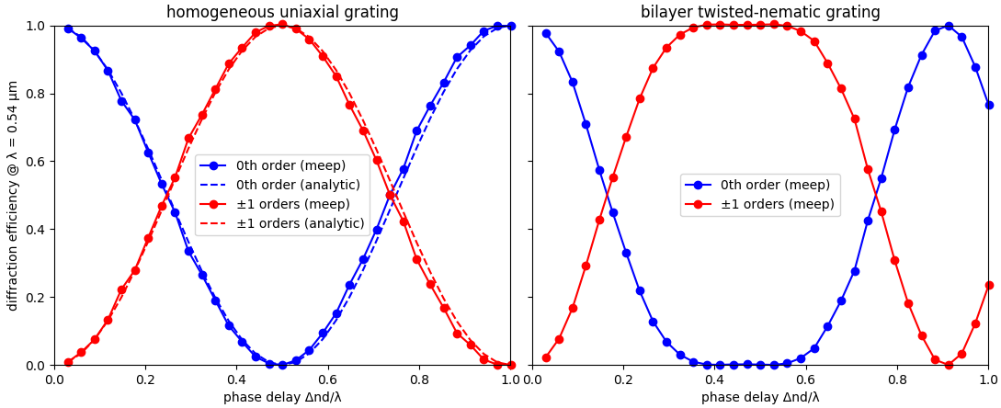
The left figure shows good agreement between the simulation results and analytic theory for the homogeneous uniaxial grating. Approximately 6% of the power in the input planewave is lost due to reflection from the grating. This value is an average over all phase delays. The total transmittance is therefore around 94%. The twisted-nematic grating, with results shown in the right figure, produces ±1 diffraction orders with nearly-constant peak transmittance over a broader bandwidth around $\Delta nd/\lambda=0.5$ than the homogeneous uniaxial polarization grating. This is consistent with results from the reference. The average reflectance and transmittance for the twisted-nematic grating are similar to those for the homogeneous uniaxial grating.


Finally, we demonstrate that when $\Delta nd/\lambda=0.5$ a circular-polarized planewave input produces just a single ±1 diffraction order. To create a $\mathcal{J}_z + i\mathcal{J}_y$ circular-polarized planewave current source involves overlapping two linear-polarized planewave sources for $\mathcal{J}_y$ and $\mathcal{J}_z$ where the `amplitude` property of one of the sources is the imaginary number `1j` in order to create a phase offset of 90°:

```py
sources = [mp.Source(mp.GaussianSource(fcen,fwidth=0.05*fcen),
                     component=mp.Ez,
                     center=src_pt,
                     size=mp.Vector3(0,sy,0)),
           mp.Source(mp.GaussianSource(fcen,fwidth=0.05*fcen),
                     component=mp.Ey,
                     center=src_pt,
                     size=mp.Vector3(0,sy,0),
                     amplitude=1j)]
```

Note: when imparting a phase offset using a complex `amplitude`, it is *not* necessary to set `force_complex_fields=True` in the `Simulation` constructor since the real part of the current *includes* the phase offset.

The figure below shows a snapshot of $E_z$ for four different cases: phase delays ($\Delta nd/\lambda$) of 0.5 and 1.0, and circular-polarized planewave sources of $E_z + iE_y$ and $E_z - iE_y$. The empty regions on the cell sides are PMLs. The thin solid black line denotes the boundary between the grating (on the left) and air. As expected, for $\Delta nd/\lambda=0.5$ there is just a single ±1 diffraction order which depends on the chirality of the input planewave (this is not the case for a linear-polarized planewave). The angle of this diffracted order (±4.8°) agrees with the analytic result. Snapshots of $E_y$ are similar.


![](../images/polarization_grating_diffraction_orders.png#center)


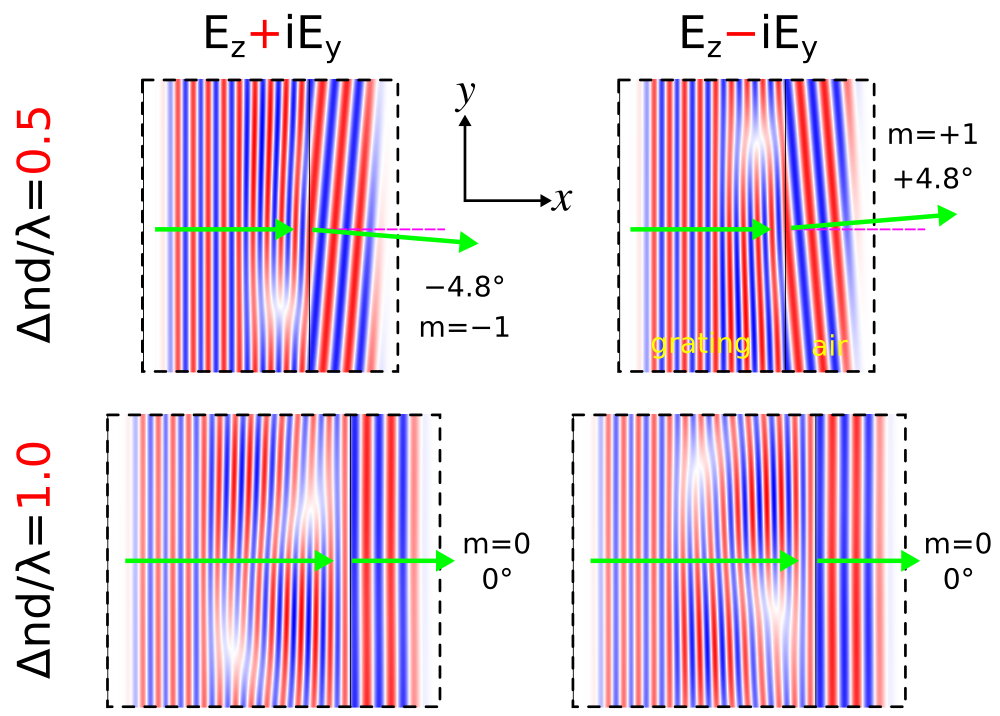
For computing the mode coefficient of an [elliptically polarized](https://en.wikipedia.org/wiki/Elliptical_polarization) mode in 3d, one approach is to first compute the mode coefficients of two orthogonal linearly polarized modes ($\mathcal{S}$ and $\mathcal{P}$ polarizations) separately using the [`DiffractedPlanewave`](../Python_User_Interface.md#diffractedplanewave) object which is passed as the `bands` parameter to `get_eigenmode_coefficients`. The complex mode coefficients for these two polarizations can then be combined in post-processing via a linear combination to compute the mode coefficient for any arbitrary elliptically polarized mode.  Alternatively, you can specify an elliptical polarization directly in a single `DiffractedPlanewave` object by supplying both $\mathcal{S}$ and $\mathcal{P}$ amplitudes with the desired relative phase.