1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
---
# Gyrotropic Media
---
In this example, we will perform simulations with gyrotropic media. See [Materials](../Materials.md#gyrotropic-media) for more information on how gyrotropy is supported.
[TOC]
### Faraday Rotation
Consider a uniform gyroelectric medium with bias vector $\mathbf{b} = b \hat{z}$. In the frequency domain, the *x* and *y* components of the dielectric tensor have the form
$$\epsilon = \begin{bmatrix}\epsilon_\perp & -i\eta \\ i\eta & \epsilon_\perp \end{bmatrix}$$
The skew-symmetric off-diagonal components give rise to [Faraday rotation](https://en.wikipedia.org/wiki/Faraday_effect): when a plane wave linearly polarized along *x* is launched along the gyrotropy axis *z*, the polarization vector will precess around the gyrotropy axis as the wave propagates. This is the principle behind [Faraday rotators](https://en.wikipedia.org/wiki/Faraday_rotator), devices that act as one-way valves for light.
A plane wave undergoing Faraday rotation can be described by the complex ansatz
$$\begin{bmatrix}E_x \\ E_y\end{bmatrix} = E_0 \begin{bmatrix}\cos(\kappa_c z) \\ \sin(\kappa_c z)\end{bmatrix} e^{i(kz-\omega t)}$$
where $\kappa_c$ is the Faraday rotation (in radians) per unit of propagation distance. Substituting this into the frequency domain Maxwell's equations, with the above dielectric tensor, yields
$$|\kappa_c| = \omega \sqrt{\frac{\mu}{2} \, \left(\epsilon_\perp - \sqrt{\epsilon_\perp^2 - \eta^2}\right)}$$
We model this phenomenon in the simulation script [faraday-rotation.ctl](https://github.com/NanoComp/meep/blob/master/scheme/examples/faraday-rotation.ctl). First, we define a gyroelectric material:
```scm
(define-param epsn 1.5) ; background permittivity
(define-param f0 1.0) ; natural frequency
(define-param g0 1e-6) ; damping rate
(define-param sn 0.1) ; sigma parameter
(define-param b0 0.15) ; magnitude of bias vector
(set! default-material
(make dielectric
(epsilon epsn)
(E-susceptibilities
(make gyrotropic-lorentzian-susceptibility
(frequency f0)
(sigma sn)
(gamma g0)
(bias (vector3 0 0 b0))))))
```
The `gyrotropic-lorentzian-susceptibility` object has a `bias` argument that takes a `vector3` specifying the gyrotropy vector. In this case, the vector points along *z*, and its magnitude (which specifies the precession frequency) is determined by the variable `b0`. The other arguments play the same role as in an ordinary (non-gyrotropic) [Lorentzian susceptibility](Material_Dispersion.md).
Next, we set up and run the Meep simulation.
```scm
(define-param tmax 100)
(define-param L 20.0)
(define-param fsrc 0.8)
(define-param src-z -8.5)
(set-param! resolution 50)
(set! geometry-lattice (make lattice (size 0 0 L)))
(set! pml-layers (list (make pml (thickness 1.0) (direction Z))))
(set! sources (list
(make source
(src (make continuous-src (frequency fsrc)))
(component Ex)
(center (vector3 0 0 src-z)))))
(run-until tmax
(to-appended "efields"
(at-end output-efield-x)
(at-end output-efield-y)))
```
The simulation cell is one pixel wide in the *x* and *y* directions, with periodic boundary conditions. [PMLs](../Perfectly_Matched_Layer.md) are placed in the *z* direction. A `ContinuousSource` emits a wave whose electric field is initially polarized along *x*.
After running the simulation, the `ex` and `ey` datasets in `faraday-rotation-efields.h5` contain the values of $\mathbf{E}_x$ and $\mathbf{E}_y$. These are plotted against *z* in the figure below:

We see that the wave indeed rotates in the *x*-*y* plane as it travels.
Moreover, we can compare the Faraday rotation rate in these simulation results to theoretical predictions. In the [gyrotropic Lorentzian model](../Materials.md#gyrotropic-media), the ε tensor components are given by
$$\epsilon_\perp = \epsilon_\infty + \frac{\omega_n^2 \Delta_n}{\Delta_n^2 - \omega^2 b^2}\,\sigma_n(\mathbf{x}),\;\;\; \eta = \frac{\omega_n^2 \omega b}{\Delta_n^2 - \omega^2 b^2}\,\sigma_n(\mathbf{x}), \;\;\;\Delta_n \equiv \omega_n^2 - \omega^2 - i\omega\gamma_n$$
From these expressions, we can calculate the rotation rate $\kappa_c$ at the operating frequency, and hence find the $\mathbf{E}_x$ and $\mathbf{E}_y$ field envelopes for the complex ansatz given at the top of this section. As shown in the figure below, the results are in excellent agreement:
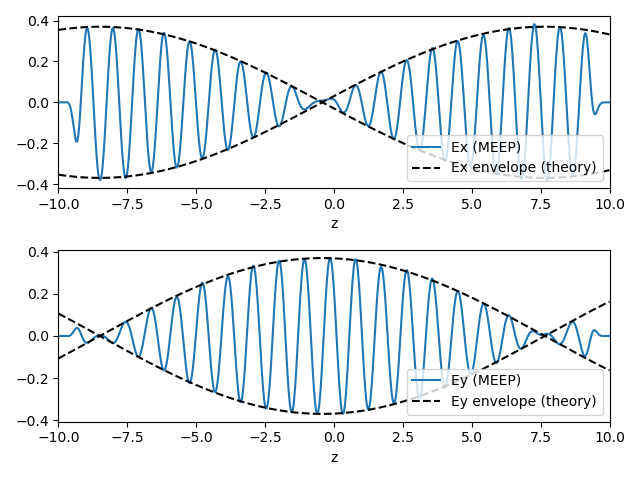
|