# cotengrust

`cotengrust` provides fast rust implementations of contraction ordering
primitives for tensor networks or einsum expressions. The two main functions
are:

- `optimize_optimal(inputs, output, size_dict, **kwargs)`
- `optimize_greedy(inputs, output, size_dict, **kwargs)`

The optimal algorithm is an optimized version of the `opt_einsum` 'dp'
path - itself an implementation of https://arxiv.org/abs/1304.6112.

There is also a variant of the greedy algorithm, which runs `ntrials` of greedy,
randomized paths and computes and reports the flops cost (log10) simultaneously:

- `optimize_random_greedy_track_flops(inputs, output, size_dict, **kwargs)`


## Installation

`cotengrust` is available for most platforms from
[PyPI](https://pypi.org/project/cotengrust/):

```bash
pip install cotengrust
```

or if you want to develop locally (which requires [pyo3](https://github.com/PyO3/pyo3)
and [maturin](https://github.com/PyO3/maturin)):

```bash
git clone https://github.com/jcmgray/cotengrust.git
cd cotengrust
maturin develop --release
```
(the release flag is very important for assessing performance!).


## Usage

If `cotengrust` is installed, then by default `cotengra` will use it for its
greedy, random-greedy, and optimal subroutines, notably subtree
reconfiguration. You can also call the routines directly:

```python
import cotengra as ctg
import cotengrust as ctgr

# specify an 8x8 square lattice contraction
inputs, output, shapes, size_dict = ctg.utils.lattice_equation([8, 8])

# find the optimal 'combo' contraction path
%%time
path = ctgr.optimize_optimal(inputs, output, size_dict, minimize='combo')
# CPU times: user 13.7 s, sys: 83.4 ms, total: 13.7 s
# Wall time: 13.7 s

# construct a contraction tree for further introspection
tree = ctg.ContractionTree.from_path(
    inputs, output, size_dict, path=path
)
tree.plot_rubberband()
```
![optimal-8x8-order](https://github.com/jcmgray/cotengrust/assets/8982598/f8e18ff2-5ace-4e46-81e1-06bffaef5e45)


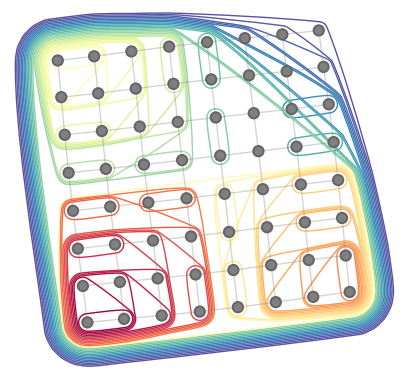
## Benchmarks

The following benchmarks illustrate performance and may be a useful comparison point for other implementations.

---

First, the runtime of the optimal algorithm on random 3-regular graphs,
with all bond sizes set to 2, for different `mimimize` targets:

<img src="https://github.com/user-attachments/assets/e1b906a8-e234-4558-b183-7141c41beb24" width="400">

Taken over 20 instances, lines show mean and bands show standard error on mean. Note how much easier it is
to find optimal paths for the *maximum* intermediate size or cost only (vs. *total* for all contractions).
While the runtime generally scales exponentially, for some specific geometries it might reduce to
polynomial.

---

For very large graphs, the `random_greedy` optimizer is appropriate, and there is a tradeoff between how
long one lets it run (`ntrials`) and the best cost it achieves. Here we plot these for various
$N=L\times L$ square grid graphs, with all bond sizes set to 2, for different `ntrials`
(labelled on each marker):

<img src="https://github.com/user-attachments/assets/e319b5cf-25ea-4273-aa0f-4f3acb3beaa6" width="400">

Again, data is taken over 20 runs, with lines and bands showing mean and standard error on the mean.
In most cases 32-64 trials is sufficient to achieve close to convergence, but for larger or harder
graphs you may need more. The empirical scaling of the random-greedy algorithm is very roughly
$\mathcal{O}(N^{1.5})$ here.

---

The depth 20 sycamore quantum circuit amplitude is a standard benchmark nowadays, it is generally
a harder graph than the 2d lattice. Still, the random-greedy approach can do quite well due to its
sampling of both temperature and `costmod`:

<img src="https://github.com/user-attachments/assets/17b34e11-a755-4ed7-b88b-39b9e5424cfc" width="400">

Again, each point is a `ntrials` setting, and the lines and bands show the mean and error on the mean
respectively, across 20 repeats. The dashed line shows the roughly best known line from other more
advanced methods.

---


## API

The optimize functions follow the api of the python implementations in `cotengra.pathfinders.path_basic.py`.

```python
def optimize_optimal(
    inputs,
    output,
    size_dict,
    minimize='flops',
    cost_cap=2,
    search_outer=False,
    simplify=True,
    use_ssa=False,
):
    """Find an optimal contraction ordering.

    Parameters
    ----------
    inputs : Sequence[Sequence[str]]
        The indices of each input tensor.
    output : Sequence[str]
        The indices of the output tensor.
    size_dict : dict[str, int]
        The size of each index.
    minimize : str, optional
        The cost function to minimize. The options are:

        - "flops": minimize with respect to total operation count only
          (also known as contraction cost)
        - "size": minimize with respect to maximum intermediate size only
          (also known as contraction width)
        - 'max': minimize the single most expensive contraction, i.e. the
          asymptotic (in index size) scaling of the contraction
        - 'write' : minimize the sum of all tensor sizes, i.e. memory written
        - 'combo' or 'combo={factor}` : minimize the sum of
          FLOPS + factor * WRITE, with a default factor of 64.
        - 'limit' or 'limit={factor}` : minimize the sum of
          MAX(FLOPS, alpha * WRITE) for each individual contraction, with a
          default factor of 64.

        'combo' is generally a good default in term of practical hardware
        performance, where both memory bandwidth and compute are limited.
    cost_cap : float, optional
        The maximum cost of a contraction to initially consider. This acts like
        a sieve and is doubled at each iteration until the optimal path can
        be found, but supplying an accurate guess can speed up the algorithm.
    search_outer : bool, optional
        If True, consider outer product contractions. This is much slower but
        theoretically might be required to find the true optimal 'flops'
        ordering. In practical settings (i.e. with minimize='combo'), outer
        products should not be required.
    simplify : bool, optional
        Whether to perform simplifications before optimizing. These are:

        - ignore any indices that appear in all terms
        - combine any repeated indices within a single term
        - reduce any non-output indices that only appear on a single term
        - combine any scalar terms
        - combine any tensors with matching indices (hadamard products)

        Such simpifications may be required in the general case for the proper
        functioning of the core optimization, but may be skipped if the input
        indices are already in a simplified form.
    use_ssa : bool, optional
        Whether to return the contraction path in 'single static assignment'
        (SSA) format (i.e. as if each intermediate is appended to the list of
        inputs, without removals). This can be quicker and easier to work with
        than the 'linear recycled' format that `numpy` and `opt_einsum` use.

    Returns
    -------
    path : list[list[int]]
        The contraction path, given as a sequence of pairs of node indices. It
        may also have single term contractions if `simplify=True`.
    """
    ...


def optimize_greedy(
    inputs,
    output,
    size_dict,
    costmod=1.0,
    temperature=0.0,
    simplify=True,
    use_ssa=False,
):
    """Find a contraction path using a (randomizable) greedy algorithm.

    Parameters
    ----------
    inputs : Sequence[Sequence[str]]
        The indices of each input tensor.
    output : Sequence[str]
        The indices of the output tensor.
    size_dict : dict[str, int]
        A dictionary mapping indices to their dimension.
    costmod : float, optional
        When assessing local greedy scores how much to weight the size of the
        tensors removed compared to the size of the tensor added::

            score = size_ab / costmod - (size_a + size_b) * costmod

        This can be a useful hyper-parameter to tune.
    temperature : float, optional
        When asessing local greedy scores, how much to randomly perturb the
        score. This is implemented as::

            score -> sign(score) * log(|score|) - temperature * gumbel()

        which implements boltzmann sampling.
    simplify : bool, optional
        Whether to perform simplifications before optimizing. These are:

        - ignore any indices that appear in all terms
        - combine any repeated indices within a single term
        - reduce any non-output indices that only appear on a single term
        - combine any scalar terms
        - combine any tensors with matching indices (hadamard products)

        Such simpifications may be required in the general case for the proper
        functioning of the core optimization, but may be skipped if the input
        indices are already in a simplified form.
    use_ssa : bool, optional
        Whether to return the contraction path in 'single static assignment'
        (SSA) format (i.e. as if each intermediate is appended to the list of
        inputs, without removals). This can be quicker and easier to work with
        than the 'linear recycled' format that `numpy` and `opt_einsum` use.

    Returns
    -------
    path : list[list[int]]
        The contraction path, given as a sequence of pairs of node indices. It
        may also have single term contractions if `simplify=True`.
    """

def optimize_simplify(
    inputs,
    output,
    size_dict,
    use_ssa=False,
):
    """Find the (partial) contracton path for simplifiactions only.

    Parameters
    ----------
    inputs : Sequence[Sequence[str]]
        The indices of each input tensor.
    output : Sequence[str]
        The indices of the output tensor.
    size_dict : dict[str, int]
        A dictionary mapping indices to their dimension.
    use_ssa : bool, optional
        Whether to return the contraction path in 'single static assignment'
        (SSA) format (i.e. as if each intermediate is appended to the list of
        inputs, without removals). This can be quicker and easier to work with
        than the 'linear recycled' format that `numpy` and `opt_einsum` use.

    Returns
    -------
    path : list[list[int]]
        The contraction path, given as a sequence of pairs of node indices. It
        may also have single term contractions.
    """
    ...

def optimize_random_greedy_track_flops(
    inputs,
    output,
    size_dict,
    ntrials=1,
    costmod=(0.1, 4.0),
    temperature=(0.001, 1.0),
    seed=None,
    simplify=True,
    use_ssa=False,
):
    """Perform a batch of random greedy optimizations, simulteneously tracking
    the best contraction path in terms of flops, so as to avoid constructing a
    separate contraction tree.

    Parameters
    ----------
    inputs : tuple[tuple[str]]
        The indices of each input tensor.
    output : tuple[str]
        The indices of the output tensor.
    size_dict : dict[str, int]
        A dictionary mapping indices to their dimension.
    ntrials : int, optional
        The number of random greedy trials to perform. The default is 1.
    costmod : (float, float), optional
        When assessing local greedy scores how much to weight the size of the
        tensors removed compared to the size of the tensor added::

            score = size_ab / costmod - (size_a + size_b) * costmod

        It is sampled uniformly from the given range.
    temperature : (float, float), optional
        When asessing local greedy scores, how much to randomly perturb the
        score. This is implemented as::

            score -> sign(score) * log(|score|) - temperature * gumbel()

        which implements boltzmann sampling. It is sampled log-uniformly from
        the given range.
    seed : int, optional
        The seed for the random number generator.
    simplify : bool, optional
        Whether to perform simplifications before optimizing. These are:

        - ignore any indices that appear in all terms
        - combine any repeated indices within a single term
        - reduce any non-output indices that only appear on a single term
        - combine any scalar terms
        - combine any tensors with matching indices (hadamard products)

        Such simpifications may be required in the general case for the proper
        functioning of the core optimization, but may be skipped if the input
        indices are already in a simplified form.
    use_ssa : bool, optional
        Whether to return the contraction path in 'single static assignment'
        (SSA) format (i.e. as if each intermediate is appended to the list of
        inputs, without removals). This can be quicker and easier to work with
        than the 'linear recycled' format that `numpy` and `opt_einsum` use.

    Returns
    -------
    path : list[list[int]]
        The best contraction path, given as a sequence of pairs of node
        indices.
    flops : float
        The flops (/ contraction cost / number of multiplications), of the best
        contraction path, given log10.
    """
    ...

def ssa_to_linear(ssa_path, n=None):
    """Convert a SSA path to linear format."""
    ...

def find_subgraphs(inputs, output, size_dict,):
    """Find all disconnected subgraphs of a specified contraction."""
    ...
```